Az energia-lépcső 3-4,

ami megmutatja a lényeget

3.  A kettős fényelhajlás tüneménye

4.  A fény igazi sebessége

 

 

3. rész

A kettős fényelhajlás tüneménye

 

A fizikusokat már az újkor kezdetén is izgatta a kérdés, hogy vajon a fénysugarak is elgörbülnek e az égitestek mellet, miközben elhaladnak mellettük. Newton volt az első, aki úgy gondolta, hogy a fénysugár speciális részecskék áradatából tevődik össze. Ezeket a részecskékek útjuk során vonzani fogja a Nap méghozzá kétféle irányban. A fény egész útja során maga felé vonzza, de a legerősebben akkor, mikor éppen az égitest mellett halad el.

 

   Várható, hogy amikor a fény közeledik a Nap felé akkor a pályája mentén gyorsítani próbálja. Amikor pedig túlhalad rajta, akkor folytonosan visszafelé vonzza, azaz lassítani próbálja. Ha ez a folyamat létrejönne, akkor a Napnak kevesebb ideje maradna maga felé vonzani a fényt és kevésbé görbülne el a pályája. Ez egy logikus gondolatmenet, azonban ez a jelenség ne lép fel. Nem várt módon erre Newton is rájött és számítása ezáltal közelebb állt a valósághoz. (Ma már tudjuk, hogy az ok a fénysebességi felső korlát.) Newton számításában tehát a fénysugár 2-szer annyira görbült meg, mintha pusztán a klasszikus mechanika alapján gondolkodott volna.

 

   Einstein is a Newton féle számértéket kapta elsőre (1914) az általános relativitáselmélet nyers változata alapján. Később azonban korrigált és egy újabb kétszeres szorzót alkalmazott. Ezt a számítást igazolta később Eddington angol csillagász az 1919-es teljes napfogyatkozás során. Ez az eredmény meghozta a relativitáselmélet fényes sikerét - bár fizikus legyen a talpán, aki képes e számítást követni vagy megismételni. A végeredményt tekintve tehát a kimért Nap melletti fényelhajlás 4-szeresnek bizonyult a naiv mechanikus számításhoz viszonyítva.

 

    A magam részéről elfogadom Newton teóriáját a 2-szeres görbülési értékkel, ami 0,87” (szögmásodperc) elhajlást jelent. Azonban én hozzáteszek egy másik gondolatot is, ami által újabb 2-szeres görbületet kapunk. Arról van szó ugyanis, hogy ha a fénysugár a görbület síkjában polarizált, akkor változó nagyságú gravitációs térben halad. A hullámhegy a Naptól távolabb van, és itt a tér gravitációs energiája kicsit nagyobb és ezért a hullámhegy kicsit gyorsabban halad. (Ezt az effektust a kékeltolódás példájában már láttuk.) A hullámvölgyek viszont jobban megközelítik a Napot. Ott a tér energiája egy kicsit kisebb, mert a térben lévő gravitációs energia negatív irányba mozdult el. Ott tehát a hullámvölgy lassabban halad. Mindezek eredménye 0,87” görbülés a Nap irányába. Fontos leszögezni, hogy a görbülési hatás egyáltalán nem függ a fény hullámhosszától. Ennek következtében a gravitációs fényelhajlás nem okozza a fénysugár színekre történő bomlását.

 

 

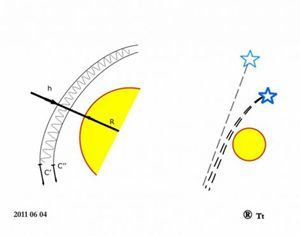
   A kétféle hatás összege 1,75” irányváltoztatás. Éppen annyi, mint azt korábban Einstein tippelte, valamint a modern mérések alapján beigazolódott. Talán csak érdekességnek tűnik, de a kétféle effektushoz tartozó 2 differenciálegyenlet határozottan különbözik egymástól. Ámde a kétféle egyenlet pontosan ugyanazt a számszerű értéket adja.

 

A fény valójában nem síkhullám amelyet az előzőkben a nap felszínére merőlegesnek és ugyanakkor párhuzamosnak is vettünk. Ahogyan ezt már korábban az aparadox nevű honlapomon ismertettem a fényhullám valójában térbeli csavarvonal (helix) mely két egymás körül forgó részecskéből áll és fénysebességgel halad előre. Ennek síkvetülete szinuszhullám bármely irányból, így például az előbb említett főirányból nézve is. Mint láttuk, e két szinuszhullámra szépen kijött a fényelhajlás ismert értéke. Igen ám, de mi van a csavarvonal többi általános pontjával? Természetesen ezekre is ugyanaz a képlet és szabály vonatkozik, hiszen a fényelhajlás mértéke a reá vonatkozó differenciál egyenletek szerint nem függenek a hullámhossztól, illetve a hullám kitérésétől.

 

 

4. rész

A fény igazi sebessége

 

Az utóbbi évszázadokban a fénysugár sebességét nagyon sokszor és nagy igyekezettel megmérték. A mérések egyre pontosabbá váltak, és ma már csak az utolsó 2-3 számjegye kétséges. Ez valószínűleg sokáig így is marad, ezért a tudomány áttért a számítási módszerre, és a c₀ sebességet az e₀ és m₀ paraméterekből számolja ki:

c = (e₀ * m₀)^-1/2

 

 

Az itt megjelenített c-vel jelölt fénysebességet azonban helytelenül nevezték el vákuumbeli fénysebességnek. Igaz ugyan, hogy a méréseket vákuum-csőben végezték, ámde ez itt történt talajszinten, azaz a Föld gravitációs energiájával csökkentett tér-részben. (Természetesen ez a sajnálatos félreértés a többi vákuum paraméterre, jelesül az e₀ és m₀ paraméterekre is vonatkozik.) A 0 gravitációs térben a vákuum energiája valamint a fény sebessége a legnagyobb. A valódi vákuumbeli fénysebességet pedig a Change energia-lépcső segítségével fogjuk kiszámítani.

 

Érzékletes példa lesz, ha gondolatban veszünk egy konyhai mérleghez tartozó 1 kilogrammos mérlegsúlyt. Mennyivel lesz több ennek az energiája ha eltávolítjuk a Földtől a végtelen messzeségbe? Régóta ismert a tömeg gravitációs energiájának számítási képlete egy tömeg végtelenből a véges R sugarú és M tömegű bolygóra érkezve:

E_grav=mMG/R=1 * 6*10²⁴ * 6,67*10^-11/6,37*10⁶=63 MJ (mega-joule)

 

Ha a fenti energia átalakulna hővé, akkor a mérlegsúly hőmérséklete 140000 kelvin fok lenne. A számításnál figyelembe vettem a meglehetősen jelentéktelen olvadáshőt (0,267 MJ) azonban nem tudtam figyelembe venni a párolgáshőt, mivel az túl nagy (6070 MJ). Ez azt jelenti, hogy a mérlegsúly csak részben párolog el, mialatt földet ér. Pedig a vas forráspontja nem tűnik magasnak (2750 oC). Ebben az energia-gödörben kisebb az energiaszint, továbbá a hozzá tartozó fizikai paraméterek is: e₀, m₀, c₀, h₀, stb.

 

 

 

A fentiekben tehát azt állítjuk, hogy az alap értéknek használt fizikai állandók nem az elméleti értéket mutatják. Talán egyszer a gravitációtól mentes térben lévő elméleti értékeket is ki lehetne mérni, de bőven megbízhatunk a számított többletek értékében is. Mindössze a gravitációs energia különbségét kellett kiszámítani a földfelszín és a végtelen között, melyből a De/e₀ arányszám már könnyen kiadódik.

 

A vákuumban mérhető alapállandók:

 

A táblázatban látható értékek (alapállandók) megváltozott számértékeire a piros színezés hívja fel a figyelmet. A fénysebesség hivatalos c értéke esetén a tudomány nem szokta kiírni a tizedesjegyeket, mert az utolsó néhány egész szám is kissé bizonytalan. Ámde akármennyi is lesz majd a pontos végeredmény a földfelszíni mérések és számítások alapján az soha nem lesz tökéletes. Elvileg tökéletes csak akkor lesz, ha még hozzáadják a táblázatban megadott 0,210 m/s többlet-sebességet.

 

            Paradigmaváltást a fizikában - most!            

 

Kelt: 2019 október hó

 

Tassi Tamás

fejlesztőmérnök

hobby-fizikus

aparadox.hupont.hu

 

 

   <<  Vissza                                                                      Tovább  >>

          A proton és a neutron belső szerkezete            Energia-lépcső II.

 

 

Oldal: Energia-lépcső 3-4
Paradigmaváltás a fizikában! - © 2008 - 2024 - paradigma-valtas.hupont.hu

A HuPont.hu az ingyen weblap készítés központja, és talán a legjobb. Ingyen weblap

ÁSZF | Adatvédelmi Nyilatkozat